Представљање графова и њихова елементарна својства
Два најчешћа начина представљања графова су преко матрица повезаности и преко листа суседства.
Матрица повезаности (суседства)
Нека је \(\vert V\vert=n\) и \(V=\{v_1,v_2,\ldots,v_n\}\). Матрица повезаности тј. матрица суседства графа \(G\) је квадратна матрица \(A=(a_{ij})\) реда \(n\), са елементима \(a_{ij}\) који су једнаки 1 ако и само ако \((v_i,v_j)\in E\); остали елементи матрице \(A\) су нуле. Ако је граф неусмерен, матрица \(A\) је симетрична. Врста \(i\) ове матрице је дакле низ дужине \(n\) чија је \(j\)-та координата једнака \(1\) ако из чвора \(v_i\) води грана ка чвору \(v_j\), односно \(0\) у противном. Недостатак матрице повезаности је то што она увек заузима простор величине \(n^2\), независно од тога колико грана има граф. Ако је број грана у графу мали, већина елемената матрице повезаности биће нуле. Ако се за представљање графа користи матрица повезаности, сложеност операције уклањања неке гране из графа је \(O(1)\) и испитивање да ли су два чвора у графу повезана је такође \(O(1)\).
У језику C++ можемо употребити следећу репрезентацију матрице.
bool A[MAX][MAX];или, ако не знамо унапред број чворова тј. ако број чворова \(n\) сазнајемо тек у фази извршавања програма
vector<vector<bool>> A(n);
for (int i = 0; i < n; i++)
A[i].resize(n);Листе повезаности (суседства)
Уместо да се и све непостојеће гране експлицитно представљају у матрици повезаности, могу се формирати повезане листе од јединица из \(i\)-те врсте, \(i=1,2,\ldots,n\). Овај други начин представљања графа зове се листа повезаности, односно листа суседства. Сваком чвору придружује се листа (или низ), која садржи све гране суседне чвору (односно гране ка суседним чворовима). Граф је представљен низом листа (тј. низова).
На пример, граф усмерен граф приказан на слици се може представити следећим листама суседа.
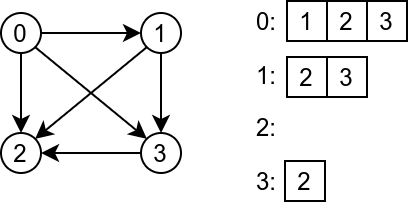
Треба напоменути да иако име тако сугерише, имплементација овакве репрезентације графа не мора бити заснована на листама, већ се уместо повезаних листи може користити динамички низ или нека врста балансираних бинарних дрвета или пак хеш табела. У већини наредних алгоритама сматраћемо да је граф са којим радимо динамички и да је задат листом повезаности.
У језку C++ можемо употребити следећу репрезентацију.
vector<vector<int>> susedi(n);Нову грану можемо додати помоћу
susedi[cvorOd].push_back(cvorDo);Ако је граф неусмерен, тада се за сваку грану додају два податка.
susedi[cvorA].push_back(cvorB);
susedi[cvorB].push_back(cvorA);Итерацију кроз све суседне гране чвора можемо остварити помоћу
for (int cvorDo : susedi[cvorOd])
...Оваква репрезентација омогућава да се у времену \(O(1)\) нађу суседи сваког појединачног чвора у графу.
Матрице повезаности омогућавају да се у времену \(O(1)\) испита да ли између два чвора постоји грана. С друге стране, листе повезаности омогућавају да се једноставније пронаћу сви суседи неког датог чвора. Листе повезаности су меморијски ефикасније за графове са малим бројем грана (њихова меморијска сложеност је \(O(V + E)\), за разлику од матрица повезаности чија је меморијска сложеност \(O(V^2)\)). У пракси се често ради са графовима који имају знатно мање грана од максималног могућег броја (\(n(n-1)/2\) неусмерених, односно \(n(n-1)\) усмерених грана), и тада је ефикасније користити листе повезаности.
Репрезентација листа повезаности помоћу једног низа
Ако је граф статички, односно нису дозвољена уметања и брисања, онда се цео граф може представити помоћу једног низа целих бројева, на следећи начин. У основи је и даље репрезентација у облику листа повезаности. Користи се низ дужине \(\vert V\vert +\vert E\vert\). Првих \(\vert V\vert\) чланова низа су придружени чворовима. Компонента низа придружена чвору \(v_i\) садржи индекс почетка списка чворова суседних чвору \(v_i\), \(i=1,2,\ldots,n\). На слици је на једном примеру приказано представљање графа помоћу матрице повезаности и преко једног низа у коме се чувају све листе повезаности.
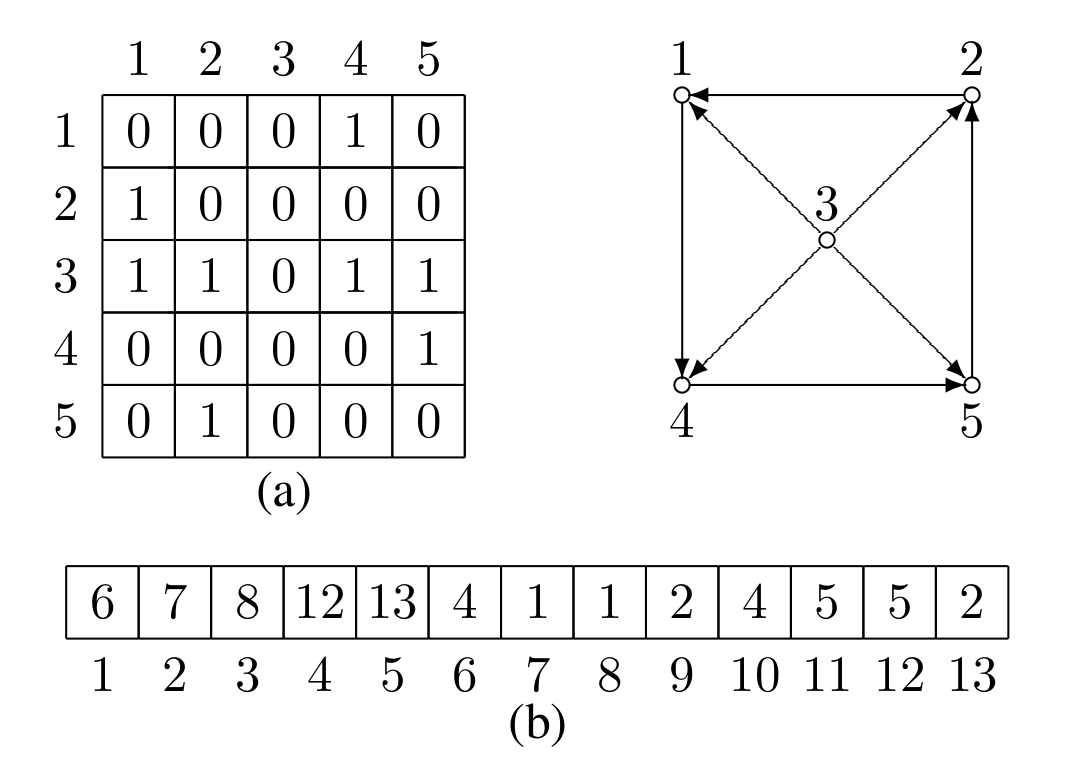
Треба поменути да постоје и други начини за представљање графа, као што су матрице или листе инциденције где се за сваку грану чува информација са којим чворовима је инцидентна.
Представљање графова и њихова елементарна својства
Два најчешћа начина представљања графова су преко матрица повезаности и преко листа суседства.
Матрица повезаности (суседства)
Нека је \(\vert V\vert=n\) и \(V=\{v_1,v_2,\ldots,v_n\}\). Матрица повезаности тј. матрица суседства графа \(G\) је квадратна матрица \(A=(a_{ij})\) реда \(n\), са елементима \(a_{ij}\) који су једнаки 1 ако и само ако \((v_i,v_j)\in E\); остали елементи матрице \(A\) су нуле. Ако је граф неусмерен, матрица \(A\) је симетрична. Врста \(i\) ове матрице је дакле низ дужине \(n\) чија је \(j\)-та координата једнака \(1\) ако из чвора \(v_i\) води грана ка чвору \(v_j\), односно \(0\) у противном. Недостатак матрице повезаности је то што она увек заузима простор величине \(n^2\), независно од тога колико грана има граф. Ако је број грана у графу мали, већина елемената матрице повезаности биће нуле. Ако се за представљање графа користи матрица повезаности, сложеност операције уклањања неке гране из графа је \(O(1)\) и испитивање да ли су два чвора у графу повезана је такође \(O(1)\).
У језику C# можемо употребити следећу репрезентацију матрице.
bool[,] A = new bool[n, n];где је \(n\) број чворова у графу.
Листе повезаности (суседства)
Уместо да се и све непостојеће гране експлицитно представљају у матрици повезаности, могу се формирати повезане листе од јединица из \(i\)-те врсте, \(i=1,2,\ldots,n\). Овај други начин представљања графа зове се листа повезаности, односно листа суседства. Сваком чвору придружује се листа (или низ), која садржи све гране суседне чвору (односно гране ка суседним чворовима). Граф је представљен низом листа (тј. низова).
На пример, граф усмерен граф приказан на слици се може представити следећим листама суседа.

Треба напоменути да иако име тако сугерише, имплементација овакве репрезентације графа не мора бити заснована на листама, већ се уместо повезаних листи може користити динамички низ или нека врста балансираних бинарних дрвета или пак хеш табела. У већини наредних алгоритама сматраћемо да је граф са којим радимо динамички и да је задат листом повезаности.
У језку C# можемо употребити следећу репрезентацију.
List<int>[] susedi = new List<int>[n];
for (int cvorOd = 0; cvorOd < n; cvorOd++)
susedi[cvorOd] = new List<int>();Нову грану тада можемо додати помоћу
susedi[cvorOd].push_back(cvorDo);Ако је граф неусмерен, тада се за сваку грану додају два податка.
susedi[cvorA].push_back(cvorB);
susedi[cvorB].push_back(cvorA);Итерацију кроз све суседне гране чвора можемо остварити помоћу
foreach (int cvorDo in susedi[cvorOd])
...Оваква репрезентација омогућава да се у времену \(O(1)\) нађу суседи сваког појединачног чвора у графу.
Матрице повезаности омогућавају да се у времену \(O(1)\) испита да ли између два чвора постоји грана. С друге стране, листе повезаности омогућавају да се једноставније пронаћу сви суседи неког датог чвора. Листе повезаности су меморијски ефикасније за графове са малим бројем грана (њихова меморијска сложеност је \(O(V + E)\), за разлику од матрица повезаности чија је меморијска сложеност \(O(V^2)\)). У пракси се често ради са графовима који имају знатно мање грана од максималног могућег броја (\(n(n-1)/2\) неусмерених, односно \(n(n-1)\) усмерених грана), и тада је ефикасније користити листе повезаности.
Репрезентација листа повезаности помоћу једног низа
Ако је граф статички, односно нису дозвољена уметања и брисања, онда се цео граф може представити помоћу једног низа целих бројева, на следећи начин. У основи је и даље репрезентација у облику листа повезаности. Користи се низ дужине \(\vert V\vert +\vert E\vert\). Првих \(\vert V\vert\) чланова низа су придружени чворовима. Компонента низа придружена чвору \(v_i\) садржи индекс почетка списка чворова суседних чвору \(v_i\), \(i=1,2,\ldots,n\). На слици је на једном примеру приказано представљање графа помоћу матрице повезаности и преко једног низа у коме се чувају све листе повезаности.

Треба поменути да постоје и други начини за представљање графа, као што су матрице или листе инциденције где се за сваку грану чува информација са којим чворовима је инцидентна.
